1. ReLU 및 그 변종
이전에 다룬 내용을 요약해 보겠습니다.
시그모이드 함수를 사용하고 기울기가 0.25 미만일 경우 역전파 과정에서 입력 레이어 쪽으로 가면 역전파가 제대로 이루어지지 않는 기울기 손실 문제가 발생할 수 있다.
이를 완화하기 위해 히든 레이어 활성화 함수로 ReLU 또는 ReLU의 변환 함수를 사용합니다.
2. 그라데이션 클리핑
그래디언트 클리핑은 그래디언트 값을 클리핑하여 그래디언트 폭주를 방지하는 기술입니다. RNN(반복 신경망)에서 특히 유용합니다. 역전파 중에 기울기가 매우 커질 수 있으므로 기울기 값은 임계값을 초과하지 않도록 기울기 클리핑에 의해 제한됩니다. 즉, 임계값만큼 크기를 줄입니다.
3. 가중치 초기화
1) 자비에 초기화
2) 그는 초기화
4. 배치 정규화
1) 내부 공변량 이동
학습 과정에서 계층별로 데이터의 분포가 다른 현상을 말한다. 이전 레이어의 학습으로 인해 이전 레이어의 가중치가 변경되면 현재 레이어로 공급되는 입력 데이터의 분포와 현재 레이어가 학습한 시점의 분포가 다르게 된다.
2) 배치 정규화
배치 정규화는 문자 그대로 배치 단위로 정규화하는 것을 의미합니다. Batch Normalization은 각 레이어의 Boosting 기능 전에 수행됩니다. 스택 정규화를 요약하려면 입력을 0으로 평균화한 다음 정규화합니다. 그리고 데이터를 확장하고 이동합니다.
배치 정규화를 사용할 때 각 계층에 대해 입력 분포 및 정규화가 수행됩니다. 시그모이드 함수와 하이퍼볼릭 탄젠트 함수의 도함수는 입력값이 증가할수록 감소하는 것을 확인하였으며, 이때 스택 정규화를 사용하면 입력값이 있는 부분에 국부화되기 때문에 기울기 손실 문제가 크게 완화된다. 미분 값은 활성화 함수에 있습니다. 이와 관련하여 그래디언트 분포가 안정화 되었기 때문에 더 큰 학습률을 사용해도 그래디언트 폭주나 발산이 발생하지 않아 학습 속도를 향상시킬 수 있고 가중치 초기화에 덜 민감하다.
또한 각 배치에 대해 평균 및 표준 편차가 계산되고 사용되므로 데이터에 약간의 노이즈가 추가될 수 있습니다. 과적합을 방지하는 효과가 있습니다.
그러나 배치 정규화는 추가 계산을 생성하기 때문에 테스트 데이터를 예측할 때 실행 시간이 느려질 수 있습니다.
3) 배치 정규화 제한
스택 정규화는 스택 단위로 계속 정규화되지만 스택 크기가 너무 작으면 제대로 작동하지 않을 수 있습니다. 간단한 예로 배치 크기가 1이면 분산이 0이 되어 학습에 방해가 될 수 있습니다. 따라서 스택 정규화를 적용할 때 특정 스택 크기를 갖는 것이 좋습니다.
그리고 RNN에 적용하기 어렵다. RNN은 특정 시점에 다른 통계를 가지므로 RNN에 배치 정규화를 적용하기 어렵습니다. 따라서 RNN에 적용하기 쉽고 배치 크기에 의존하지 않는 레이어 정규화를 도입합니다.
5. 계층 정규화
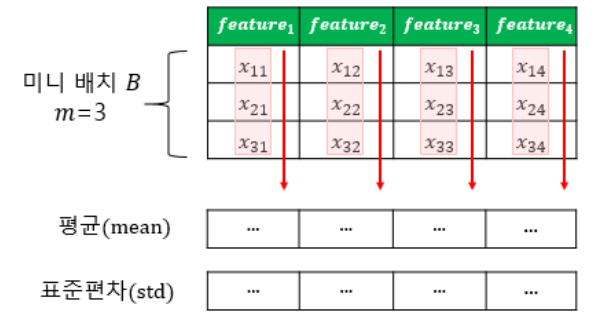
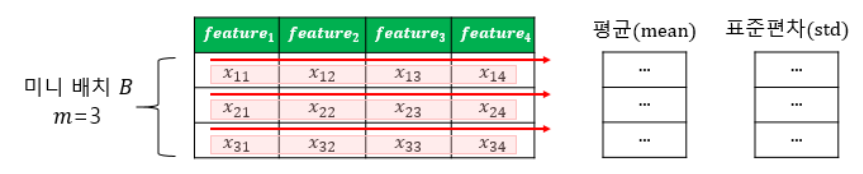
왼쪽에는 배치 정규화의 시각화가 있습니다. m이 3이고 특징 수가 4일 때 배치 정규화.
미니 배치는 동일한 수의 기능을 가진 여러 패턴을 의미합니다.
계층 정규화는 미니 배치의 크기에 민감하지 않으며 RNN과 같은 반복 신경망에 적용하기에 적합합니다. 또한 학습이 안정적이고 빠르기 때문에 학습을 안정화하고 기울기 손실 문제를 완화하여 다양한 신경망 구조에 적용할 수 있습니다.

ofekp.jpg?type=w800)

